Graph Analytics Workloads¶
What is Graph Analytics¶
A graph is a data structure composed of vertices (or nodes) connected by edges. Graphs can represent many real-world data, such as social networks, transportation networks, and protein interaction networks, as shown in the following figure.

Examples of graphs.¶
In general, any computation on graph data can be considered graph analytics. The objective of graph analytics is to uncover and utilize the structure of graphs, providing insights into the relationships and connections between different elements in graphs. Computation patterns in graph analytics can vary significantly: some involve only a small number of vertices/edges, while others access a large portion or even all vertices/edges of a graph. In GraphScope, we refer to the former as graph traversal and the latter as graph analytics, unless specified otherwise.
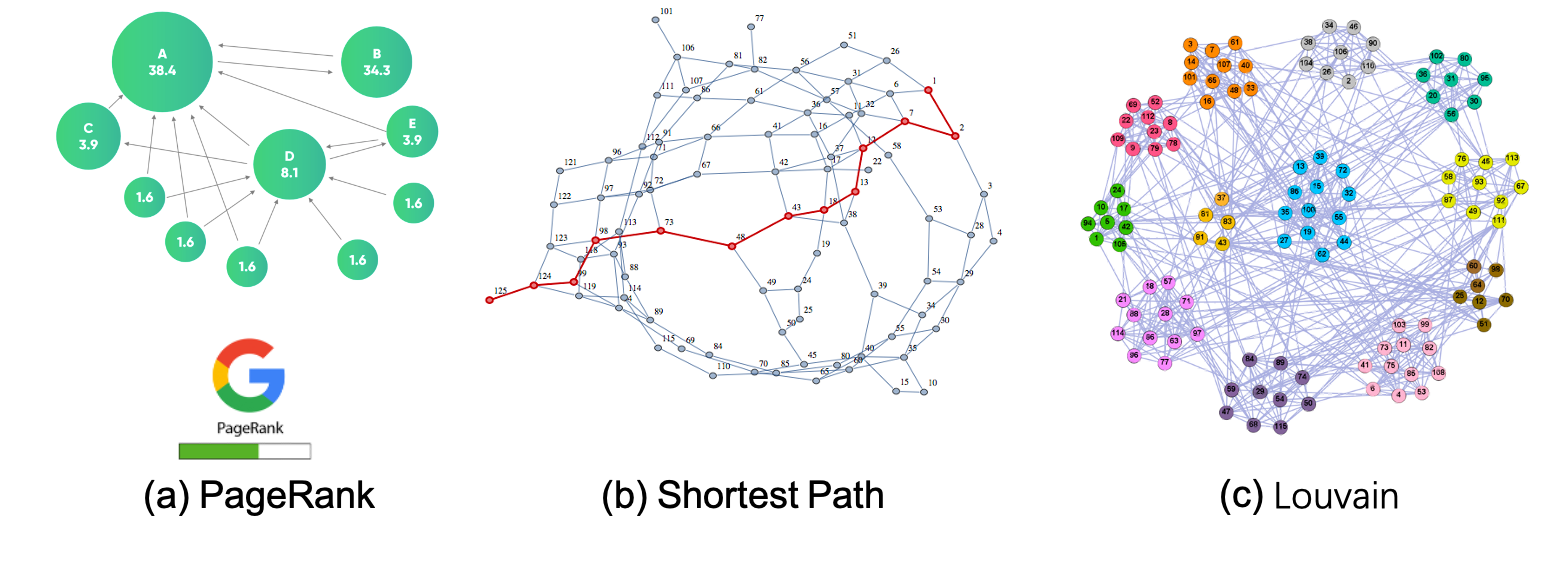
There are various types of graph analytics algorithms, which typically iterate over a large portion or all vertices/edges of a graph to discover hidden insights within the graph data. Common graph analytics algorithms include general analytics algorithms (e.g., PageRank, shortest path, and maximum flow), community detection algorithms (e.g., maximum clique/bi-clique, connected components, Louvain, and label propagation), and graph mining algorithms (e.g., frequent structure mining and graph pattern discovery). Below, we provide several examples to illustrate how graph analytics algorithms operate.
The PageRank algorithm measures the importance of each vertex in a graph by iteratively counting the number and importance of its neighbors. This helps determine a rough estimate of a vertex’s importance. Specifically, the PageRank computation consists of multiple iterations, with each vertex initially assigned a value indicating its importance. During each iteration, vertices sum the values of their neighbors pointing to them and update their own values accordingly.
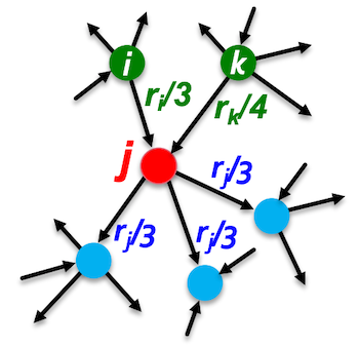
PageRank algorithm (https://snap-stanford.github.io/cs224w-notes/network-methods/pagerank).¶
The shortest path problem aims to find the most efficient path between two vertices by minimizing the sum of the weights of its constituent edges. Several well-known algorithms, such as Dijkstra’s algorithm and Bellman–Ford algorithm, have been proposed to solve this problem. For instance, Dijkstra’s algorithm selects a single vertex as the “source” vertex and attempts to find the shortest paths from the source to all other vertices in the graph. The computation of Dijkstra’s algorithm involves multiple iterations. In each iteration, a vertex with a known shortest path to the source is selected, and the shortest path values of its neighbors are updated, as demonstrated in the following figure.
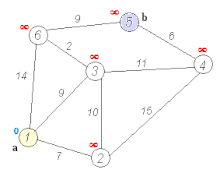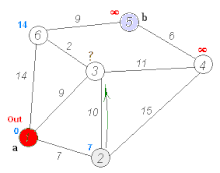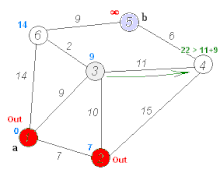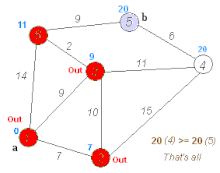
Dijkstra’s algorithm (https://en.wikipedia.org/wiki/Dijkstra’s_algorithm).¶
Community detection algorithms (e.g., Louvain) aim to identify groups of vertices that are more densely connected internally than with other vertices in the graph. These algorithms work by having each vertex repeatedly send its label to its neighbors and update its own label based on specific rules after receiving labels from its neighbors. After multiple iterations, vertices that are densely connected internally will have the same or similar labels.
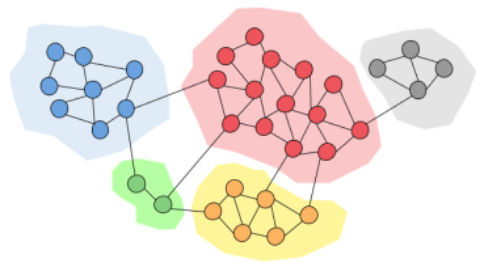
Community detection algorithm (https://towardsdatascience.com/community-detection-algorithms-9bd8951e7dae).¶
The examples above demonstrate how graph analytics algorithms analyze properties of vertices and edges within a graph. In real-world applications, many problems can be modeled as graph analytics problems. For instance, Google Search represents websites and their interconnections as a graph, applying the PageRank algorithm to identify the most important websites on the Internet. Similarly, a city’s road map can be modeled as a graph, with the shortest path algorithm assisting in path planning for logistics and delivery services. By considering social media users as a graph, community detection techniques (e.g., Louvain) can help discover users with shared interests and maintain strong connections between them.
Applications of graph analytics.¶
Challenges of Graph Analytics on Large Graphs¶
Based on our experience, processing graph data and utilizing frameworks (systems) for graph data processing present the following challenges:
Handling large-scale and complex graph data
The majority of real-world graph data is large-scale, heterogeneous, and attributed. For instance, modern e-commerce graphs often contain billions of vertices and tens of billions of edges, with various types and rich attributes. Representing and storing such graph data is a nontrivial task.
Diverse programming models/languages
Numerous graph processing systems have been developed to manage graph analytics algorithms. These systems employ different programming models (e.g., vertex-centric model and PIE model) and programming languages (e.g., C++, Java, and Python). Consequently, users often face steep learning curves.
Demand for high performance
The efficiency and scalability of processing large graphs remain limited. While current systems have significantly benefited from years of optimization work, they still encounter efficiency and/or scalability issues. Achieving superior performance when dealing with large-scale graph data is highly sought after.
What can GraphScope Do¶
In GraphScope, the Graph Analytics Engine (GAE) tackles the aforementioned challenges by managing graph analytics algorithms in the following manner:
Distributed graph data management
GraphScope represents graph data as a property graph model and automatically partitions large-scale graphs into subgraphs (fragments) distributed across multiple machines in a cluster. It also provides user-friendly interfaces for loading graphs, making graph data management easier. For more details on managing large-scale graphs, refer to this.
Various programming models/languages support
GraphScope supports both the vertex-centric model (Pregel) and PIE (PEval-IncEval-Assemble) programming model. These models are widely used in existing graph processing systems. For more information, refer to our introductions to Pregel and PIE models.
GraphScope provides SDKs for multiple languages, allowing users to write custom algorithms in C++, Java, or Python. For more details on developing customized algorithms, check out our tutorials.
Optimized high-performance runtime
GAE achieves high performance through an optimized analytical runtime, employing techniques such as pull/push dynamic switching, cache-efficient memory layout, and pipelining. We have compared GraphScope with state-of-the-art graph processing systems on the LDBC Graph Analytics Benchmark, and the results show that GraphScope outperforms other graph systems.