Programming Model: FLASH¶
FLASH is a distributed programming model for programming a broad spectrum of graph algorithms, including clustering, centrality, traversal, matching, mining, etc. FLASH follows the vertex-centric philosophy, but it moves a step further for stronger expressiveness by providing flexible control flow, the operations on arbitrary vertex sets and beyond-neighborhood communication. FLASH makes diverse complex graph algorithms easy to write at the distributed runtime. The algorithms expressed in FLASH take only a few lines of code, and provide a satisfactory performance.
Motivation¶
The majority of recent graph processing frameworks only focus on a handful of fix-point graph algorithms such as breadth-first search, PageRank, shortest path, etc. It leaves the distributed computation of a large variety of graph algorithms suffering from low efficiency, limited expressiveness, or high implementation complexity with existing frameworks. The well-known vertex-centric implementation of a graph algorithm follows a common iterative, single-phased and value-propagation-based (short of ISVP) pattern: the algorithm runs iteratively until convergence, and in each iteration, all vertices receive messages from their neighbors to update their own states, then they send the updated states as messages to the neighbors for the next iteration. Such high-level abstraction brings productivity to some extent to users, however, at the sacrifice of expressiveness. This abstraction, while designed specifically for the ISVP algorithms, is almost infeasible to be applied to a large variety of algorithms that are not of the kind. At the same time, modern graph scenarios bring in the needs of more advanced and complex graph algorithms, which poses a big challenge for existing graph processing frameworks.
After investigating representative distributed graph algorithms, including many non-ISVP ones, we have distilled three requirements that are critical for programming them efficiently and productively in a distributed context, namely (1) flexible control flow; (2) operations on vertex subsets; and (3) beyond-neighborhood communication. However, existing graph frameworks all fall short in meeting these requirements. Therefore, there is a need to design a new programming model which fulfills all of the three requirements, and supports to program in a distributed context.
The FLASH Programming Model¶
Overview¶
The FLASH programming model is based on Ligra to inherit its support for the requirements of flexible control flow and operations on vertex subsets. By further enabling beyond-neighborhood communication, FLASH improves the expressiveness for programming a diverse variety of graph algorithms. Since Ligra is a single-machine parallel library, FLASH makes an extension to the distributed context, for which it must handle communication, synchronization, data races and task scheduling. To do so, a middleware called FlashWare is proposed that hides all the above details for distribution, and provides the capability to apply multiple system optimizations automatically and adaptively at the runtime.
We have implemented 70+ graph algorithms with FLASH for 40+ different commonly used applications, and we can now program much more succinct codes using the FLASH programming interfaces, which also helps productivity. The evaluation results demonstrate FLASH’s capability of expressing many advanced algorithms (takes up to 92% less lines of code), while providing a satisfactory performance at the same time.
FLASH API¶
FLASH is a functional programming model specific for distributed graph processing. It follows the Bulk Synchronous Parallel (BSP) computing paradigm with each of the primary functions constitutes a single superstep. It utilizes the VertexSubset type which represents a set of vertices of the graph G, containing a set of indices for all vertices in this set. The properties of vertices are maintained only once for a graph, shared by all VertexSubsets. The following describes the APIs of FLASH based on VertexSubset.
VSize: This function returns the size of a VertexSubset.
size_t VSize(VertexSubset U);
VertexMap: This interface applies the map function to each vertex in U that passes the condition checking function F. The indices of the output vertices form the resulting VertexSubset. Specially, the M function could be omitted for implementing the filter semantics, with the vertex data unchanged.
VertexSubset VertexMap(VertexSubset U,
F(Vertex v) -> bool,
M(Vertex v) -> vertex);
EdgeMap: For a graph G(V,E), EdgeMap applies the update logic to the specific edges with source vertex in U and target vertex satisfying C. H represents the edge set to conduct updates, which is E in common cases. We allow the users to define arbitrary edge sets they want dynamically at runtime, even virtual edges generated during the algorithm’s execution. The edge set can be defined through defining a function which maps a source vertex index to a set of indices of the targets. We also provide some pre-defined operators for convenience, such as reverse edges, or edges with targets in a specific VertexSubset. This extension makes the communication beyond the neighborhood-exchange limitation. If a chosen edge passes the condition checking F, the map function M is applied on it. The output of the function M represents a temporary new value of the target vertex. This new value is applied immediately and sequentially if it is in the pull mode, while in the push mode, another parameter R is required to apply all the temporary new values on a specific vertex to get its final value. The updated target vertices form the output set of EdgeMap. The reduce function R should be associative and commutative to ensure correctness, or it is not required for sequentially applying M, i.e., to run EdgeMap always in the pull mode. The function C is useful in algorithms where a value associated with a vertex only needs to be updated once. FLASH provides a default function CTrue which always returns true, since the user does not need this functionality sometimes. Similarly, the F function of EdgeMap and VertexMap can also be supplied using CTrue, if it is unnecessary.
VertexSubset EdgeMap(VertexSubset U,
EdgeSet H,
F(Vertex s, Vertex d) -> bool,
M(Vertex s, Vertex d) -> Vertex,
C(Vertex v) -> bool,
R(Vertex t, Vertex d) -> Vertex);
Other auxiliary APIs are provided by FLASH for conveniently conducting set operations (including Union, Minus, Intersect, Add, Contain, etc.), traversing all vertices in a set (Traverse), getting the data value of a single vertex (GetV) and so on.
Strong Expressiveness¶
Besides expressing existing vertex-centric algorithms, FLASH provides the possibility of expressing more advanced algorithms. It is the first distributed graph processing model that satisfies all of the three critical requirements for programming non-ISVP algorithms.
(1) FLASH allows the users to define the arbitrary control flow by combining the primitives, thus it can naturally support multi-phased algorithms. In traditional vertex-centric models, these algorithms are supported in an awkward way since they only allow to provide a single user-defined function.
(2) The VertexSubset structure supplements the perspective of a single vertex, allowing to conduct updates on arbitrary vertices. Multiple vertex subsets can be maintained at the same time, they can even be defined in a recursive function. Without this feature, a framework has to start from the whole graph every time and pick up specific vertices every time.
(3) FLASH allows the users to provide the arbitrary edge set they want to transfer messages, even when the edges do not exist in the original graph. Therefore, algorithms that contain communication beyond neighborhood can be expressed intuitively.
Implementation¶
Architecture¶
The architecture of FLASH contains several main components, as shown in the following figure. The first is a code generator which takes the high-level FLASH APIs as input, and generates execution code to be run on the second component named FlashWare, which is a middleware designed and optimized for the FLASH model and is implemented based on the fundamental modules of GraphScope. The FlashWare executes the code produced by the code generator on the distributed runtime, utilizing the ability of parallel computing and communication ability of GraphScope.
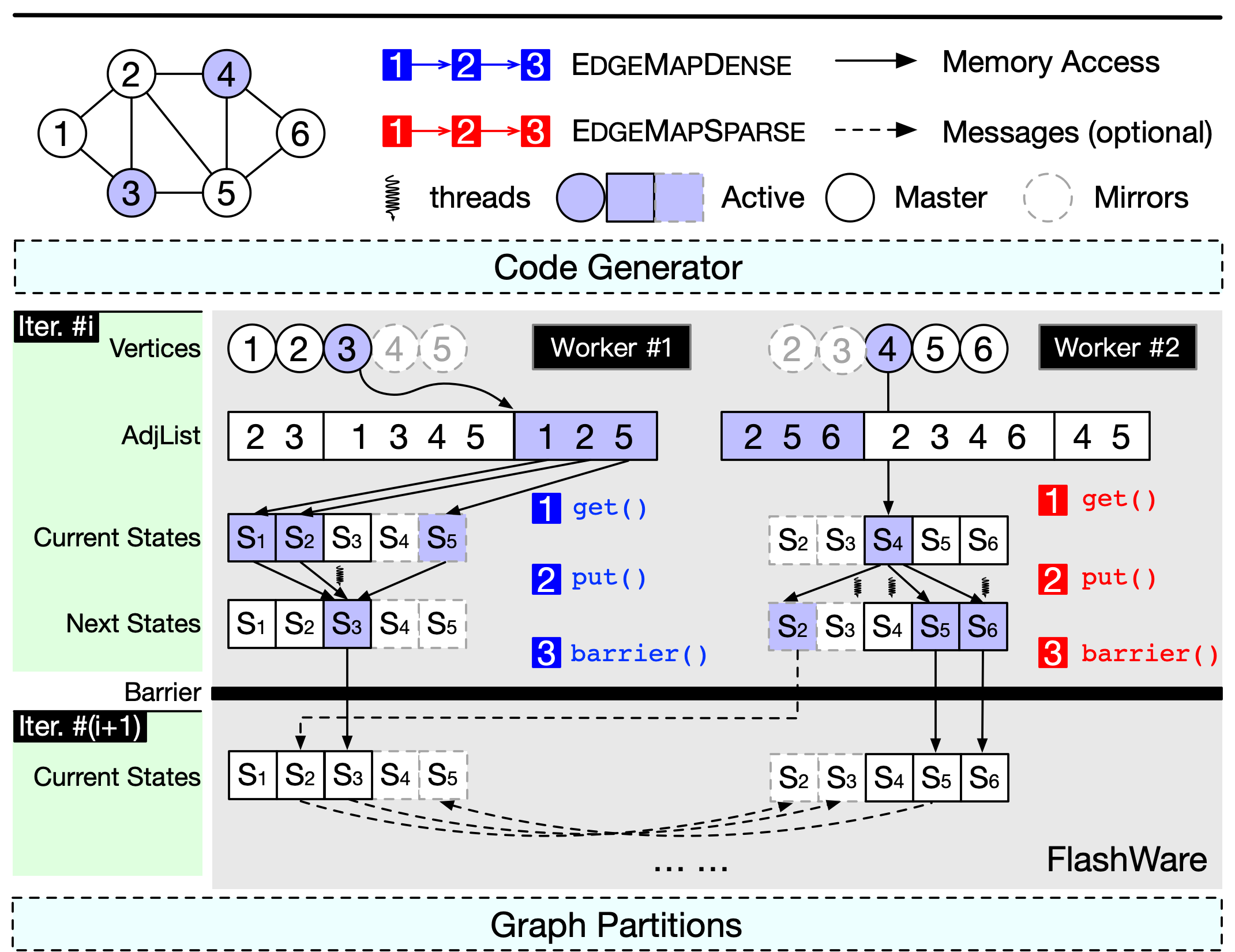
The FLASH architecture.¶
Optimizations¶
Some optimizations are introduced in the implementation of the FLASH model:
(1) During graph processing, the type of an active set may be dense or sparse, FLASH could dispatch different computation kernels for different types of the active set: the push mode for sparse active sets and the pull mode for dense active sets. This auto-switch scheme is proved to be useful for real-world graphs. Also, FLASH ’s dual mode processing is optional: users may choose to execute in only one mode through calling EdgeMapDense/EdgeMapSparse, instead of EdgeMap.
(2) FLASH utilizes separate threads to execute message passing, while other threads perform parallel vertex-centric processing, thus the computation and communication tasks are co-scheduled, leading to a performance improvement.
(3) In some cases, there are multiple vertex properties, but not all of them are critical. A property is critical only if it is accessed by other vertices, thus the update to the master need to be broadcasted to its mirrors. On the contrary, if it is only useful in local computation, it is not critical. This optimization reduces the size of a single message from the total size of all properties to only that of critical properties.
(4) Another way to eliminate redundant messages is to communicate with only the necessary mirrors. For normal graph applications, the messages are transferred along the edges. Therefore, a vertex should only broadcast to the partitions that contain at least one neighbor of this vertex. Only in the cases that the programmers define virtual edges for EdgeMap, which beyond the scope of E, FlashWare synchronizes the update on a vertex to all partitions, thus this optimization is disabled.
Built-in Algorithms¶
We have implemented 70+ graph algorithms with FLASH for 40+ different common problems, including clustering, centrality, traversal, matching, mining, etc. In addition, we are continuously adding more algorithms in FLASH, and we encourage the users to develop their own algorithms with the FLASH model. The built-in algorithms with the FLASH model in GraphScope includes:
Centrality: betweenness centrality, katz centrality, eigenvector centrality, harmonic centrality, closeness centrality
Clustering and Community: clustering coefficient, fluid community (two versions), graph coloring, label propagation (two versions)
Connectivity: biconnected components (two versions), bridge detection (two versions), connected components (seven versions), strongly connected components (two versions), cut-point detection (two versions)
Core: k-core graph decomposition (two versions), k-core searching, degeneracy ordering, onion-layer ordering
Matching and Covering: maximal matching (three versions), maximal independent set (two versions), minimal vertex cover (three versions), minimal dominating set (two versions), minimal edge cover
Mining and Subgraph Matching: cycle+ triangle counting, acyclic triangle counting, cyclic triangle counting, diamond counting, in+ triangle counting, k-clique counting (two versions), out+ triangle counting, rectangle counting, triangle counting, tailed triangle counting, 2-approximation for the densest subgraph problem, 3-path counting
Ranking: ArticleRank, hyperlink-induced topic search, PageRank, personalized PageRank
Standard Measurements: diameter approximation (two versions), minimum spanning forest (two versions), k-center
Traversal: breadth-first search (four versions), random multi-source breadth-first search, single source shortest path (four versions)